안녕하세요. EdgeAI를 전공하고 있는 이민경입니다
요즘 추천시스템이 재미있어서 개인적으로 공부하고 있어요. 다양한 딥러닝 관련 공부도 하면서 논문들 읽고 재구현하는 것을 좋아해요
요즘 추천시스템이 재미있어서 개인적으로 공부하고 있어요. 다양한 딥러닝 관련 공부도 하면서 논문들 읽고 재구현하는 것을 좋아해요Email: blossominkyung@gmail.com•
추천 시스템 중 협업 필터링(Collaborative Filtering)에 대해서 알아보자.
Summary
협업 필터링이란 추천 시스템에서 많이 쓰이는 방법 중 하나로 사용자의 행동방식에 의존하여 추천하는 시스템이다. 크게 메모리 기반 협업 필터링과 모델 기반 협업 필터링으로 구분할 수 있으며, 많이 사용되는 방법은 모델 기반 중 잠재요인 기반의 협업 필터링이다.
Content
1. Collaborative Filtering
: 협업 필터링은 사용자와 아이템 간의 상호 상관 관계를 분석하여 새로운 사용자-아이템 관계를 찾아주는 것으로 사용자의 과거 경험과 행동 방식(User Behavior)에 의존하여 추천하는 시스템이다. Domain Free 방식으로 관련 지식들이 불필요하다는 장점이 있다. 그러나 협업 필터링의 대표적인 한계점들이 다음과 같이 3가지 존재한다.
•
Cold Start Problem
문자 그대로 새로운 사용자나 새로운 아이템 등장 시, 기존의 관련된 경험 또는 행동 방식이 없기 때문에 추천이 곤란해지는 문제를 뜻한다.
•
Long Tail
전체 추천 아이템으로 보이는 비율이 사용자들의 관심을 많이 받은 소수의 아이템으로 구성되어 있는 '비대칭적 쏠림 현상'이 발생하는 문제를 뜻한다.
•
계산 효율 저하
계산량이 많은 알고리즘이기에, 사용자가 증가할 수록 계산 시간이 더 길어지게 되며 효율성이 저하되는 문제를 뜻한다.
2. Memory-based CF VS Model-based CF
2.1. Memory-based collaborative filtering
( aka. 근접 이웃 방법(Neighborhood Method))
아이템들 간의 또는 사용자들 간의 관계를 계산에 중점을 두는 방식으로, 사용자가 아직 평가하지 않은 아이템을 예측하고자 한다.
1.
아이템 기반의 근접 이웃 방법 :
•
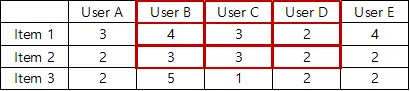
동일한 사용자의 이웃 아이템의 점수를 기반으로 해당 아이템에 대한 사용자의 선호도평가. 이미 평가했거나 상호작용한 사용자를 대상으로 하는 아이템과 유사한 아이템을 찾는 방법.
e.g Item-based Neighborhood Method
2.
사용자 기반의 근접 이웃 방법 :
•
새로운 아이템을 평가할 때, 유사한 아이템에 대해 비슷한 점수들을 매긴 다른 사용자들을 찾은 후, 해당 사용자가 상호 작용한 적 없는 아이템에 대한 아이템의 사용자 점수를 예측하는 방법.
e.g User-based Neighborhood Method
2.2. Model-based collaborative filtering
•
사용자-아이템의 숨겨진 특성(feature) 값을 계산하여 학습하는 방법으로 추천을 할 때는 학습한 모델만 있으면 된다. 따라서, 확장성과 예측 속도가 빠르다는 장점이 있으나, 모델만을 가지고 추천을 하기에 예측 정확도가 떨어질 수 있다.
•
종류: Latent Factor Models, MDP, Decision Tree, Bayesian Network 등등
이번 포스팅에서는 앞서 설명한 내용들 중 여전히 많이 사용되는 잠재요인 기반 협업 필터링(Latent Factor Model based Collaborative Filtering)에 대해서 조금 더 자세히 정리하고자 한다.
2.3. Latent Factor Model
•
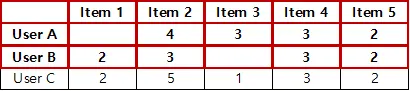
점수 패턴에서 추론된 20-100개의 벡터로 아이템들과 사용자들을 모두 특성화 하여 점수를 설명하는 방식으로 모델 기반의 협업 필터링에 속한다.
•
즉, 주어진 데이터(Matrix)로는 알 수 없는 사용자-아이템 간의 숨겨진 특성(feature)를 찾기 위해 주어진 Matrix를 사용자-잠재요인, 아이템-잠재요인으로 각각 분해하여 학습시키는 방법이다. 이때 잠재요인이 정확하게 무엇인지는 알 수 없지만, 사용자-아이템과 연관성 있는 특성(feature)들은 잠재요인이 될 수 있다.
대표적인 예로 행렬분해(Matrix Factorization) 방법이 있다.
•
데이터가 클 수록 나타나는 성능이 좋은 방법으로 현업에서도 많이 사용하는 방법 중 하나이다.
3. Singular Value Decomposition
•
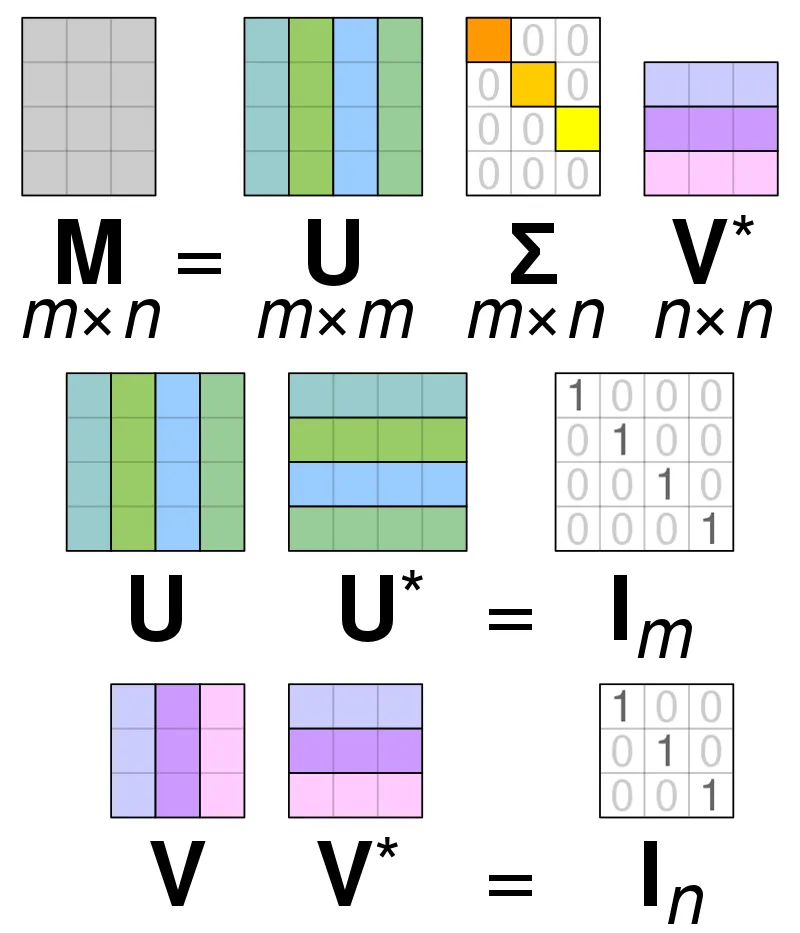
특이값 분해(SVD)는 행렬분해(Matrix Factorization)의 가장 대표적인 방법으로 행과 열의 크기가 다른 행렬에 대해서도 적용 가능하다. m x n 크기의 형렬 A를 다음과 같이 분해하는 방법이다.
•
차원 축소 기법(Dimension Reduction) 중 하나로 선형 대수학에서 특이값 분해(SVD)는 정사각형 정규행렬의 고유 분해를 극성의 확장을 통해 모든 m x n 행렬로 일반화하는 실수 또는 복소 행렬의 분해를 의미한다.
•
위의 표기 U와 V에 속하는 열 벡터를 특이 벡터(Singular Vector)라고 하는데 U의 경우 Left Singular Vector, V의 경우 Right Singular Vector라고 칭한다. 모든 특이 벡터는 서로 직교하는 성질을 가진다.
4. Principle Component Analysis
•
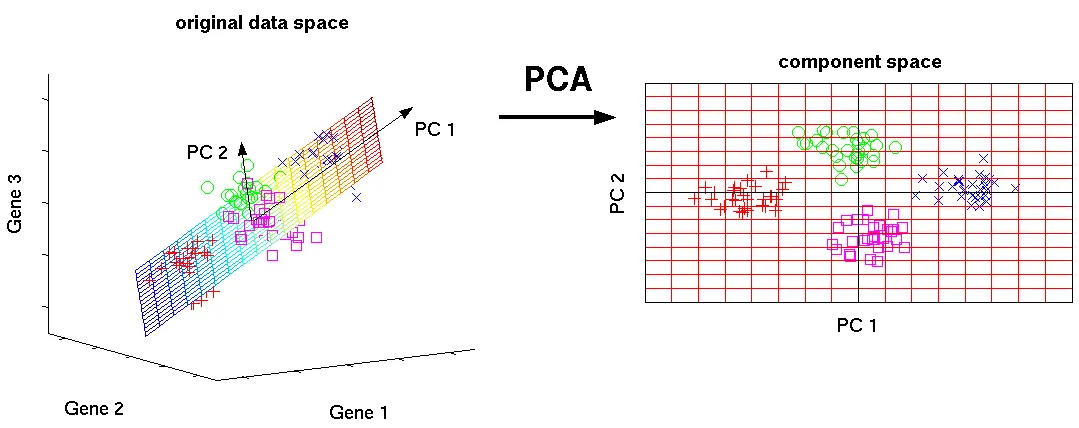
주성분 분석(PCA)도 SVD와 유사하게 차원 축소 기법(Dimension Reduction) 중 하나로 데이터에서 주성분 벡터를 찾아서 데이터의 차원을 축소시키는 방법이다.
•
PCA는 데이터의 새 좌표계의 축이 데이터의 가장 큰 분산 방향을 가리키도록 원래 데이터 공간을 회전한다. 새 변수를 주성분(PC)이라 하고 분산 순으로 정렬된다. 주성분1(PC1)은 데이터의 가장 높은 분산 방향을 나타내고 주성분2(PC2)의 뱡향은 PC1에 직교하는 나머지 분산 중 가장 높은 방향을 나타낸다.
•
가장 높은 분산을 포함하는 낮은 차원의 구성 요소 공간을 추출하기 때문에 정보 손실 없이 데이터 차원을 축소할 수 있다. 일반적으로 머신러닝 전처리에서도 많이 사용된다(속도향상).
참고자료들
(1) https://en.wikipedia.org/wiki/Collaborative_filtering
(2) https://medium.com/@kyasar.mail/recommender-systems-memory-based-collaborative-filtering-methods-b5d58ca8383
(3) http://www.cs.carleton.edu/cs_comps/0607/recommend/recommender/modelbased.html
(4) https://medium.com/analytics-vidhya/a-model-based-approach-to-build-a-recommendation-engine-1519d347cd22
(5) https://www.youtube.com/watch?v=FgakZw6K1QQ
(6) http://www.nlpca.org/pca_principal_component_analysis.html